Ordinal Logistic Regression

Ordinal Target Variable

Logistic regression is not limited to only have binary categorical target variables. Logistic regression works with target variables with any number of categories. If these categories have inherent order to them we perform ordinal logistic regression. Binary logistic regression is actually a special case of ordinal logistic regression since binary variables can only be written in two directions which is the requirement of ordinal variables. If the categories have no inherent order to them we perform nominal (or multinomial) logistic regression. Here we will discuss ordinal logistic regression.

Ordinal logistic regression models can also be used to model continuous target variables that have bounds on them however this will not be covered here.

Ordinal logistic regression models are generalizations of binary logistic regression models. In binary logistic regression we are calculating the probability that an observation has an event. In ordinal logistic regression we are calculating the probability that an observation has at most that event in an ordered list of outcomes.

We will be using the wallet data set to model the association between various factors and different levels of ethical responses to finding a wallet - returning the wallet and everything in it, returning the wallet but keeping the money found in it, keeping both the wallet and the money found inside. The variables in the data set are the following:

Variable	Description
male	indicator for a male student
business	indicator for a student enrolled at a business school
punish	how often the student was punished as a child (1 - low, 2 - moderate, 3 - high)
explain	indicator for whether explanation for punishment was given

The most common and easiest to interpret approach for ordinal logistic regression is the cumulative logit approach in the proportional odds model.

Proportional Odds Model

Instead of modeling the typical logit from binary logistic regression, we will model the cumulative logits. These cumulative logits are built off target variables with \(m\) categories. The first logit will summarize the first category compared to the rest. The second logit will summarize the first two categories compared to the rest. This continues \(m-1\) times as the last logit compares the first \(m-1\) categories to the \(m^{th}\) category. In essence, with a target variable with \(m\) categories, we are building \(m-1\) logistic regressions. This is why binary logistic regression is a special case of the ordinal logistic regression model - 2 categories in the target variable leads to one logistic regression model.

The main assumption of the proportional odds model is that although the intercept changes across the \(m-1\) models, the slope parameters on each variable stay the same. This will make the effects proportional across the different logistic regressions.

Let’s see how to build these proportional odds models in each of our softwares!

In R, we need to use the polr function instead of the glm function to perform ordinal logistic regression models. The formula piece of the function is much the same as with the glm function. The method = option specifies that we are performing a logistic regression while the data = option specifies the data frame being used.

Code

train <- wallet
train$punish <- factor(train$punish)

library(MASS)

clogit.model <- polr(factor(wallet) ~ male + business + punish + explain,
                     method = "logistic", data = train)
summary(clogit.model)


Re-fitting to get Hessian

Call:
polr(formula = factor(wallet) ~ male + business + punish + explain, 
    data = train, method = "logistic")

Coefficients:
           Value Std. Error t value
male     -1.0598     0.3274  -3.237
business -0.7389     0.3556  -2.078
punish2  -0.6276     0.4048  -1.551
punish3  -1.4031     0.4823  -2.909
explain   1.0519     0.3408   3.086

Intercepts:
    Value   Std. Error t value
1|2 -2.5679  0.4190    -6.1287
2|3 -0.7890  0.3709    -2.1273

Residual Deviance: 307.3349 
AIC: 321.3349

In the output above we see similar things to the output we have seen previously. R summarizes the model used as well as the parameter estimates of the model. The main difference in the parameter estimates is the multiple intercepts. Since we have three levels of our target variable we have two logistic regression models and therefore two intercepts.

The main question from here is whether the assumption of proportional odds actually holds. By default R doesn’t provide a global test to answer this. However, the Brant test in the brant function will test each of the variables in the separate logistic regression models to see if their slope parameters are the same.

Code

library(brant)

brant(clogit.model)

-------------------------------------------- 
Test for    X2  df  probability 
-------------------------------------------- 
Omnibus     5.46    5   0.36
male        0.51    1   0.47
business    0.58    1   0.45
punish2     0.99    1   0.32
punish3     2.81    1   0.09
explain     0.25    1   0.62
-------------------------------------------- 

H0: Parallel Regression Assumption holds

The null hypothesis for the above tests are that the assumption holds - the slopes parameter across all of the variables in the separate logistic regression models are equal. Since our p-values are above any reasonable significance level for this sample size, we have no evidence to say the assumption doesn’t hold for any of the variables.

In Python, we need to use the OrderedModel.from_formula function instead of the GLM.from_formula function to perform ordinal logistic regression models. The formula piece of the function is much the same as with the GLM function. The distri = option specifies that we are performing a logistic regression while the data = option specifies the data frame being used.

Code

from statsmodels.miscmodels.ordinal_model import OrderedModel

clogit_model = OrderedModel.from_formula('wallet ~ male + business + C(punish) + explain', data = wallet, distri = 'logit')

clogit_res = clogit_model.fit(method = 'bfgs')

Optimization terminated successfully.
         Current function value: 0.783665
         Iterations: 21
         Function evaluations: 22
         Gradient evaluations: 22

Code

clogit_res.summary()

OrderedModel Results
Dep. Variable:	wallet	Log-Likelihood:	-152.81
Model:	OrderedModel	AIC:	319.6
Method:	Maximum Likelihood	BIC:	342.5
Date:	Thu, 17 Aug 2023
Time:	09:13:03
No. Observations:	195
Df Residuals:	188
Df Model:	7

	coef	std err	z	P>\|z\|	[0.025	0.975]
C(punish)[T.2]	-0.3666	0.237	-1.544	0.123	-0.832	0.099
C(punish)[T.3]	-0.8384	0.286	-2.929	0.003	-1.399	-0.277
male	-0.6396	0.188	-3.404	0.001	-1.008	-0.271
business	-0.4573	0.208	-2.200	0.028	-0.865	-0.050
explain	0.6348	0.202	3.144	0.002	0.239	1.031
1.0/2.0	-1.5194	0.238	-6.387	0.000	-1.986	-1.053
2.0/3.0	0.0330	0.126	0.261	0.794	-0.214	0.281

In the output above we see similar things to the output we have seen previously. Python summarizes the model used as well as the parameter estimates of the model. The main difference in the parameter estimates is the multiple intercepts. Since we have three levels of our target variable we have two logistic regression models and therefore two intercepts.

The main question from here is whether the assumption of proportional odds actually holds. Unfortunately, at the time of writing this code deck, Python does not have a Brant test function to test this assumption like R or SAS.

PROC LOGISTIC is actually made to calculate ordinal logistic regression models as the binary logistic is just a special case. Notice how the code is the exact same, save one big omission. There is no event = option after the target variable since the target is just assumed to be built ordinally.

Code

proc logistic data=Logistic.Wallet;
    class punish(param=ref ref='1');
    model wallet = male business punish explain / clodds=pl;
    title 'Ordinal Logistic Regression - Ascending';
run;
quit;

In the output above we see similar things to the output we have seen previously. PROC LOGISTIC summarizes the model used, the number of observations read and used in the model, and builds a frequency table for our target variable. It then summarizes the categorical variable created in the CLASS statement followed by telling us that the model converged. It also provides us with the same global tests, type 3 analysis of effects, parameter estimates, association metrics, and odds ratios we have discussed in previous sections. The main difference in the parameter estimates is the multiple intercepts. Since we have three levels of our target variable we have two logistic regression models and therefore two intercepts.

The main question from here is whether the assumption of proportional odds actually holds. By default SAS provides us this answer with the Score test for the proportional odds assumption. The output is again highlighted below.

Code

ods html select CumulativeModelTest;
proc logistic data=Logistic.Wallet;
    class punish(param=ref ref='1');
    model wallet = male business punish explain / clodds=pl;
    title 'Ordinal Logistic Regression - Ascending';
run;
quit;

The null hypothesis for the above test is that the assumption holds - the slopes parameter across all of the variables in the separate logistic regression models are equal. Since our p-value of 0.3894 is above any reasonable significance level for this sample size, we have no evidence to say the assumption doesn’t hold.

The Score test is much like a global test across all the variables to see if the assumption holds. However, what if this test tells us the assumption doesn’t hold? Which variable(s) does it break on? Again, we go to the TEST statement in PROC LOGISTIC to answer this. We can test the same variable in different models by using an “_” followed by the model. For example, we want to know if the business variable is the same across models 1 and 2. This is given in the second TEST statement below.

Code

ods html select TestStmts;
proc logistic data=Logistic.Wallet;
    class punish(param=ref ref='1');
    model wallet = male business punish explain / unequalslopes clodds=pl;
    male: test male_1 = male_2;
    business: test business_1 = business_2;
    punish2: test punish2_1 = punish2_2;
    punish3: test punish3_1 = punish3_2;
    explain: test explain_1 = explain_2;
    title 'Ordinal Logistic Regression - Unequal Slopes';
run;
quit;

The results from the individual TEST statements agree with the global test, that there is no evidence to support there being different slope parameters for the same variables across different models. This is not surprising. These individual tests should only be run if the global test says the assumption doesn’t hold. They were performed here only for completeness.

Partial Proportional Odds Model

Although our data doesn’t have the proportional odds assumption fail in any of the variables, what would we do if it did? The partial proportional odds model is a model where some (not all) of the variables don’t follow the proportional odds assumption. If none of the variables follow the proportional odds assumption, then we should build a nominal (or multinomial) logistic regression summarized in the next section.

Let’s see how each of our softwares can build partial proportional odds models!

R uses the vglm function to perform the partial proportional odds model. The formula piece of the function is the same as previous functions used as well as the data = option. The main difference is the family = option that specifies the cumulative logit. In the cumulative option we have the parallel = F option followed by which variables we think the assumption doesn’t hold for - namely the business variable. This is just an example for completeness. According to the results from the Brant test above, all of the variables meet the assumption so we would not need the partial proportional odds model fro this dataset.

Code

library(VGAM)

plogit.model <- vglm(factor(wallet) ~ male + business + punish + explain,
                     data = train, family = cumulative(parallel = F ~ business))
summary(plogit.model)


Call:
vglm(formula = factor(wallet) ~ male + business + punish + explain, 
    family = cumulative(parallel = F ~ business), data = train)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)    
(Intercept):1  -2.6695     0.4466  -5.978 2.26e-09 ***
(Intercept):2  -0.7730     0.3678  -2.102  0.03557 *  
male            1.0707     0.3258   3.287  0.00101 ** 
business:1      0.9722     0.4789   2.030  0.04236 *  
business:2      0.6376     0.3810   1.674  0.09423 .  
punish2         0.6300     0.4008   1.572  0.11594    
punish3         1.3956     0.4727   2.952  0.00316 ** 
explain        -1.0532     0.3413  -3.086  0.00203 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2])

Residual deviance: 306.8392 on 382 degrees of freedom

Log-likelihood: -153.4196 on 382 degrees of freedom

Number of Fisher scoring iterations: 5 

No Hauck-Donner effect found in any of the estimates


Exponentiated coefficients:
      male business:1 business:2    punish2    punish3    explain 
 2.9174165  2.6438481  1.8918696  1.8776731  4.0373205  0.3488076

The above output is the same as the proportional odds model output with one difference. There are two slope parameter estimates for the business variable - one for each model. The rest of the output is the same as before.

At the time of writing this code deck, Python did not have any functionality to run partial proportional odds models.

PROC LOGISTIC can easily perform the partial proportional odds model with one additional option added on - the unequalslopes = option. Here we just list what variables needs to be built without the proportional odds assumption. Essentially, this means that those variables will have different slope parameters in the different models.

Code

ods html select ParameterEstimates;
proc logistic data=Logistic.Wallet;
    class punish(param=ref ref='1');
    model wallet = male business punish explain / unequalslopes=(business) clodds=pl;
    title 'Partial Proportional Odds Model';
run;
quit;

Interpretation

To understand the interpretation of the odds ratios in ordinal logistic regression we need to remember how the logistic regression equations are structured. Instead of modeling the typical logit from binary logistic regression, we will model the cumulative logits. These cumulative logits are built off target variables with \(m\) categories. The first logit will summarize the first category compared to the rest. The second logit will summarize the first two categories compared to the rest. This continues \(m-1\) times as the last logit compares the first \(m-1\) categories to the \(m^{th}\) category. The question really becomes what is first. Is it the largest category or the smallest category? The answer to this question will influence the interpretation of the results. If the first category is the smallest category then the categories are ascending as they build up further logistic regression models. If the first category is the largest category then the categories are descending as they build up further logistic regression models.

Both SAS and R can easily calculate descending category ordinal logistic regressions. The highest valued category is the starting point and each additional logistic regression adds the next highest valued category - building from the top down.

By default, the polr function in R builds ordinal logistic regression models in descending order of categories. To get the odds ratios from R we just exponentiate the parameter estimates from the logistic regression model.

Code

ORtable <- data.frame(OR = exp(coef(clogit.model)),
                      lower = exp(confint(clogit.model))[,1],
                      upper = exp(confint(clogit.model))[,2])
print(ORtable)

                OR      lower     upper
male     0.3465172 0.17995548 0.6522567
business 0.4776512 0.23775967 0.9626137
punish2  0.5338490 0.24246863 1.1934058
punish3  0.2458364 0.09418942 0.6315739
explain  2.8630214 1.46945567 5.6121973

Let’s see how the odds ratios are now interpreted with the descending order of categories. Odds ratios in descending ordinal logistic regressions are interpreted as having higher odds of being in a higher category for the target variable. For the male variable, males are 0.347 times more likely to have a higher value on our ethical scale as compared to non-males. A better way to think of this is that males have 65.3% lower odds of being in a higher ethical scale. Let’s remember how our scale is calculated. A value of 1 keeps the wallet and the money, 2 keeps the money but returns the wallet, and 3 returns both the money and the wallet. For the business variable, business school students have 52.2% lower odds of being in a higher ethical category as compared to non business school students.

By default, the OrderedModel function in Python builds ordinal logistic regression models in descending order of categories. To get the odds ratios from R we just exponentiate the parameter estimates from the logistic regression model.

Code

import numpy as np

100*(np.exp(clogit_res.params[0:5])-1)

C(punish)[T.2]   -30.694057
C(punish)[T.3]   -56.757756
male             -47.247554
business         -36.702404
explain           88.669331
dtype: float64

Let’s see how the odds ratios are now interpreted with the descending order of categories. Odds ratios in descending ordinal logistic regressions are interpreted as having higher odds of being in a higher category for the target variable. For the male variable, males are 0.53 times more likely to have a higher value on our ethical scale as compared to non-males. A better way to think of this is that males have 47.2% lower odds of being in a higher ethical scale. Let’s remember how our scale is calculated. A value of 1 keeps the wallet and the money, 2 keeps the money but returns the wallet, and 3 returns both the money and the wallet. For the business variable, business school students have 36.7% lower odds of being in a higher ethical category as compared to non business school students.

In SAS we need one additional option to switch our PROC LOGISTIC model from ascending to descending interpretation. The desc option will switch the order of the logistic regression estimation.

Code

ods html select CLOddsPL;
proc logistic data=Logistic.Wallet desc;
    class punish(param=ref ref='1');
    model wallet = male business punish explain / clodds=pl;
    title 'Ordinal Logistic Regression - Descending';
run;
quit;

Predictions & Diagnostics

Ordinal logistic regression has a lot of similarities to binary logistic regression:

Multicollinearity still exists
Non-convergence problems still exists
Concordance, Discordance, Tied pairs still exist and so does the \(c\) statistic
Generalized \(R^2\) remains the same

There are some inherent differences though between binary and ordinal logistic regression. A lot of the diagnostics cannot be calculated for ordinal logistic regression. ROC curves and residuals cannot typically be calculated because there is actually more than one logistic regression occurring.

Predicted probabilities are actually for each category though. Let’s see how we can get predicted probabilities from each of our softwares!

In R we have the same process of getting predicted probabilities in ordinal logistic regression as we did for binary logistic regression. The predict function will score any data set. The type = probs option is used to get individual predicted probabilities for each category.

Code

pred_probs <- predict(clogit.model, newdata = train, type = "probs")
head(pred_probs)

           1         2         3
1 0.12562481 0.3341195 0.5402557
2 0.04778463 0.1813420 0.7708734
3 0.02609095 0.1108549 0.8630542
4 0.12562481 0.3341195 0.5402557
5 0.07176375 0.2423258 0.6859105
6 0.02609095 0.1108549 0.8630542

The three variables are the individual predicted probabilities for each of the categories of our target variable. Unlike binary logistic regression where we typically did not use a cut-off of 0.5 to determine which category we predict, in ordinal logistic regression we typically pick the category with the highest probability as our predicted category.

Accuracy is typically not as high in logistic regressions with more than two categories because there are more chances for incorrect predictions. However, people do rank errors in ordinal logistic regression. For example, if the actual ethic score was 1, then a prediction of 2 is better than a prediction of 3.

In Python we have the same process of getting predicted probabilities in ordinal logistic regression as we did for binary logistic regression. The predict function will score any data set.

Code

clogit_res.model.predict(clogit_res.params)

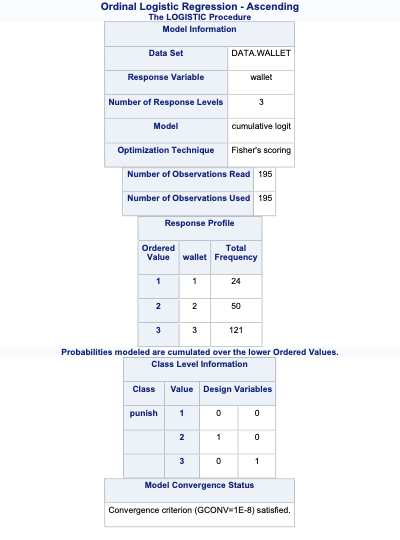
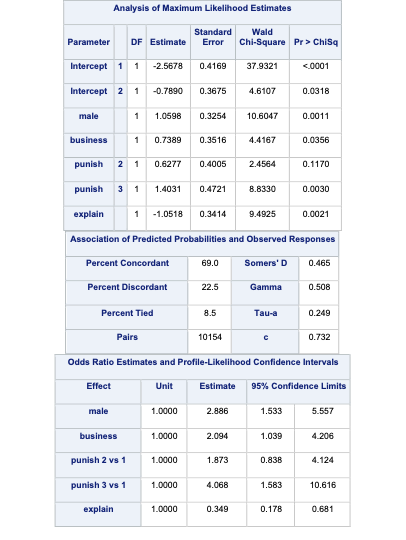
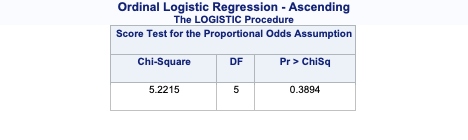
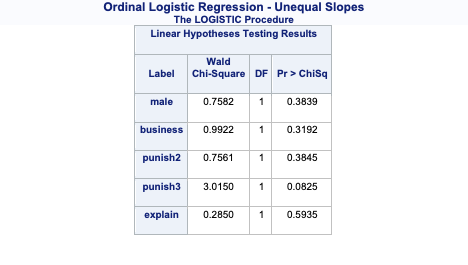
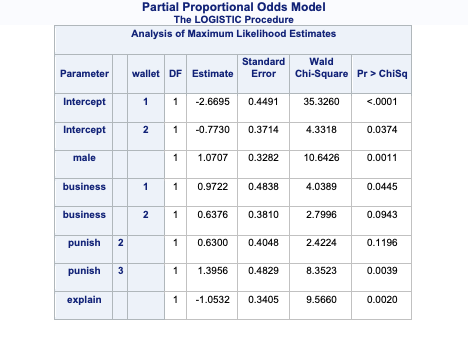
array([[0.12450334, 0.32805765, 0.54743901],
       [0.036921  , 0.18849781, 0.77458119],
       [0.01561104, 0.11560551, 0.86878345],
       [0.12450334, 0.32805765, 0.54743901],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.036921  , 0.18849781, 0.77458119],
       [0.04485704, 0.20870065, 0.74644231],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.036921  , 0.18849781, 0.77458119],
       [0.24791909, 0.38985644, 0.36222447],
       [0.66123288, 0.26515445, 0.07361267],
       [0.01561104, 0.11560551, 0.86878345],
       [0.30390383, 0.39469207, 0.30140409],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.336322  , 0.39309468, 0.27058332],
       [0.06492792, 0.25029522, 0.68477686],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.4834516 , 0.35596896, 0.16057944],
       [0.30390383, 0.39469207, 0.30140409],
       [0.30390383, 0.39469207, 0.30140409],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.12547786, 0.328959  , 0.54556314],
       [0.06492792, 0.25029522, 0.68477686],
       [0.12450334, 0.32805765, 0.54743901],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.24487445, 0.389275  , 0.36585056],
       [0.12450334, 0.32805765, 0.54743901],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.12450334, 0.32805765, 0.54743901],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.41148377, 0.37950073, 0.20901549],
       [0.30390383, 0.39469207, 0.30140409],
       [0.036921  , 0.18849781, 0.77458119],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.336322  , 0.39309468, 0.27058332],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.41332678, 0.37901579, 0.20765743],
       [0.01561104, 0.11560551, 0.86878345],
       [0.09410744, 0.2947468 , 0.61114576],
       [0.01561104, 0.11560551, 0.86878345],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.01561104, 0.11560551, 0.86878345],
       [0.04485704, 0.20870065, 0.74644231],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.06492792, 0.25029522, 0.68477686],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.24941928, 0.3901297 , 0.36045102],
       [0.24941928, 0.3901297 , 0.36045102],
       [0.24487445, 0.389275  , 0.36585056],
       [0.12547786, 0.328959  , 0.54556314],
       [0.01561104, 0.11560551, 0.86878345],
       [0.24791909, 0.38985644, 0.36222447],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.04485704, 0.20870065, 0.74644231],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.036921  , 0.18849781, 0.77458119],
       [0.336322  , 0.39309468, 0.27058332],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.04485704, 0.20870065, 0.74644231],
       [0.036921  , 0.18849781, 0.77458119],
       [0.14517644, 0.34533921, 0.50948435],
       [0.30390383, 0.39469207, 0.30140409],
       [0.06492792, 0.25029522, 0.68477686],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.66123288, 0.26515445, 0.07361267],
       [0.14517644, 0.34533921, 0.50948435],
       [0.41332678, 0.37901579, 0.20765743],
       [0.09410744, 0.2947468 , 0.61114576],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.41148377, 0.37950073, 0.20901549],
       [0.01561104, 0.11560551, 0.86878345],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.4834516 , 0.35596896, 0.16057944],
       [0.06492792, 0.25029522, 0.68477686],
       [0.04485704, 0.20870065, 0.74644231],
       [0.24791909, 0.38985644, 0.36222447],
       [0.24338899, 0.38897811, 0.3676329 ],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.14517644, 0.34533921, 0.50948435],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.01561104, 0.11560551, 0.86878345],
       [0.47771769, 0.3581683 , 0.16411401],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.036921  , 0.18849781, 0.77458119],
       [0.14517644, 0.34533921, 0.50948435],
       [0.24791909, 0.38985644, 0.36222447],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.1440992 , 0.34452838, 0.51137242],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.30390383, 0.39469207, 0.30140409],
       [0.24487445, 0.389275  , 0.36585056],
       [0.06492792, 0.25029522, 0.68477686],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.336322  , 0.39309468, 0.27058332],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.18947167, 0.3716158 , 0.43891253],
       [0.09171494, 0.29163418, 0.61665088],
       [0.24487445, 0.389275  , 0.36585056],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.41332678, 0.37901579, 0.20765743],
       [0.06492792, 0.25029522, 0.68477686],
       [0.0643303 , 0.24921245, 0.68645725],
       [0.4834516 , 0.35596896, 0.16057944],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.01561104, 0.11560551, 0.86878345],
       [0.12450334, 0.32805765, 0.54743901],
       [0.06492792, 0.25029522, 0.68477686],
       [0.47771769, 0.3581683 , 0.16411401],
       [0.30390383, 0.39469207, 0.30140409],
       [0.01561104, 0.11560551, 0.86878345],
       [0.41148377, 0.37950073, 0.20901549],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686],
       [0.01561104, 0.11560551, 0.86878345],
       [0.06492792, 0.25029522, 0.68477686],
       [0.30390383, 0.39469207, 0.30140409],
       [0.09171494, 0.29163418, 0.61665088],
       [0.12450334, 0.32805765, 0.54743901],
       [0.14517644, 0.34533921, 0.50948435],
       [0.09171494, 0.29163418, 0.61665088],
       [0.24791909, 0.38985644, 0.36222447],
       [0.336322  , 0.39309468, 0.27058332],
       [0.09410744, 0.2947468 , 0.61114576],
       [0.12547786, 0.328959  , 0.54556314],
       [0.01561104, 0.11560551, 0.86878345],
       [0.24941928, 0.3901297 , 0.36045102],
       [0.01561104, 0.11560551, 0.86878345],
       [0.14517644, 0.34533921, 0.50948435],
       [0.06492792, 0.25029522, 0.68477686],
       [0.06492792, 0.25029522, 0.68477686]])

In PROC LOGISTIC we have the same process of getting predicted probabilities in ordinal logistic regression as we did for binary logistic regression. The OUTPUT statement will score the training set, while the SCORE statement will score the validation data set. The predprobs = I option is used to get individual predicted probabilities for each category.

Code

ods html select Association;
proc logistic data=Logistic.Wallet;
    class punish(param=ref ref='1');
    model wallet = male business punish explain;
    output out=pred predprobs=I;
run;
quit;

proc print data=pred (obs = 5);
run;

proc freq data=pred;
   tables _from_*_into_ / plots=none;
   title 'Crosstabulation of Observed Responses by Predicted Responses';
run;
quit;

The IP variables are the individual predicted probabilities for each of the categories of our target variable. Unlike binary logistic regression where we typically did not use a cut-off of 0.5 to determine which category we predict, in ordinal logistic regression we typically pick the category with the highest probability as our predicted category. The FROM and INTO variables are the actual target variable category and the predicted category for the target respectively.

To see how the predicted categories compare with the actual target categories we can use PROC FREQ with a TABLES statement on the FROM and INTO variables.